Wave-length of sound in Hertz versus Closest Packing of Sphere versus Yards/Inches.

• In our some of our computer software it seems legal that for instance 14.4 (1.44 actually) yards is equal to 258 hz. Likewise 7.2 yards is equal to 52 hz.
  
  
• 258 hz then further, corresponds to number of outer-most layer of spheres in a 8 frequency Octahedron.
  
  
• Similar 52 hz from 7.2 yards , seems to correspond to number of spheres in the outer-most layer of a 5 frequency Tetrahedron.
  
  
• 1.44 is a "harmonic" of the maximum speed-of-light in vacuum, 7.2 half of that..
  
  According to the works of Bruce Cathie they are also supposed to represent, ..144 one half matter / anti-matter cycle, and 72 1/4th of one such wave-cycle.
  
  
• These are just two hz-values / harmonic values that correspond to 2nf²+2.
  
  
• If we pick 102 hz; from a 5 frequency Tetrahedron we get 3.6 yards.(3.6 a Harmonic of 360).
  
  
• Similar 252 hz from 6 frequency Vector Equilibrium gives us 1.5 yards.(1.5 a Harmonic used in spacing of the grid-lines.).
  
  
• Another one 386 hz give 0.96 yards or 2.9 feet.
  
  
• The conversion is a little bit more complicated than straight from yards to hertz of course, but it's probably something about how sound travels across any given yard.
  
  The equation finally got checked, and used was hertz=v/371.52, probably. Where v is 1.44 / 7.2 and so hence forth.
  
  
• These are now just 5 values; random and non-random tested, and there are literally countless and infinite, more from 2nf²+2.
  
  Still we are optimistic, as Synergetics was employed in the former article as well, on figuring square..pressure / magnetic field-density per cm².
  
  
• Problem is now; what logic can we gather out of this? How can we make a system out if this?..
  
  
• Regardless, these pointers may mean that the (grid-)) system bears some relation to Synergetics.
  
  
• EDIT: Not all values fit. We could not get a could fix for 432 into hertz, for instance. Why, we don't know yet.
  
  

Here is a bit of 2nf²:

Tetrahedron.	Octahedron.	Cube.	VE
[4,	6,	8,	12]
[10,	18,	26,	42]
[20,	38,	56,	92]
[34,	66,	98,	162]
[52,	102,	152,	252]
[74,	146,	218,	362]
[100,	198,	296,	492]
[130,	258,	386,	642]
[164,	326,	488,	812]
[202,	402,	602,	1002]
[244,	486,	728,	1212]
[290,	578,	866,	1442]
[340,	678,	1016,	1692]
[394,	786,	1178,	1962]
[452,	902,	1352,	2252]

Spy-satellite.

Code-name George Orwell figured out about the satellite"... 13.3 meters in diameter.

Or 43.63 feet = 523.622047 inches. Interesting numbers those, because if you divide Pi by 6 (the multiplying harmonic value as stated by Cathie) the value is similar (3.1415 / 6 = 0.5235833333). Working backwards...

523.5833333 inches = 43.6319 Feet or 13.2990167 metres."

We also figured out that if we had 14.4 yards which give harmonic 432 in feet , then the diameter should be harmonic 1.317. Because 14.4 yards is 1.317 meters. And calculating we find that harmonic 432 feet correspond to 258 from 2nf²+2 where geometric configuration n=2 , and layer/frequency f=8, so an 8 frequency Octahedron. This might not seem to fit with Orwell's calculations, but it does. If we take (pi/6)/0.432 we have ≃ 1.212034202773839 that corresponds to these values:



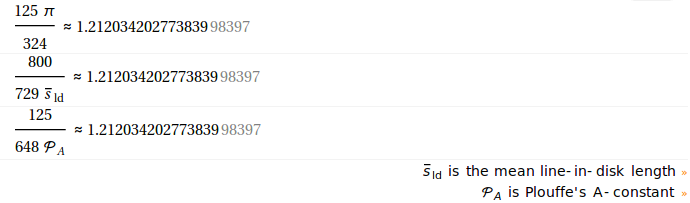
Also we have written the following about it: "And 14.4 yards == 4.32 feet.., 1.317 meters; re: US spy satellite... 13.3-13.17=0.13 (And 1.317*(6076/6000)=1.333682))

... Edit: Harmonic 14348907 (log(14348907) / log(27) == 5) when you somehow convert it to hertz...miles and hertz aren't really compatible the computer program says, but it still gives a result: "Frequency v of a photon in a vacuum from v = c/lambada = 0.013 hz"; there's one vague link to the missing 0.13 between the two (values above).

Thanks to "George Orwell" who initially brought up the issue about the satellite.

INDEX

© Krister F. Lilleland 2008-2017