Boolean and(&) function on 288 plotted shows a wave-form: (of matter and anti-matter's two phases) and other technical "wave-graphs".. ..shown..

• (We have only tried this with the "logical" geometric values 60 and 90 plus 288, if this is exciting or not, or mean anything? It could be indicated of zero-point fluctuation or something like that within maybe a carrier-wave.)
  
  
• This is the waveform generated when [288&x] is plotted for x in range 1 to 1024, and it "pulses" within a pulse as can be seen clear. It may look like a polarity-shifting AC curve/diagram (some have noted it might be what is called 4-phase.):
  
  
• And it also more importantly maybe show the normal "Matter / Anti-matter's" shifting pulses.
  
  
• Also just maybe it may be sought of as a linear representation of an outward spiral..
  
  
• Check here for all the exact boolean values (listed)..
  
  
  
  
• This one (above) is fine an the digits are for 288:
  
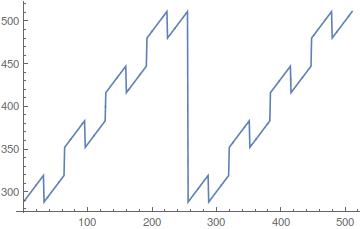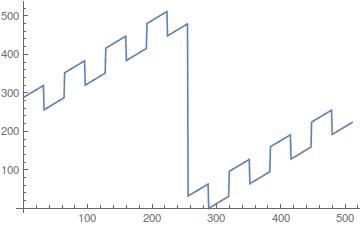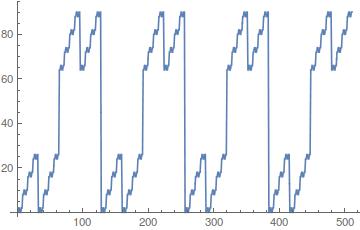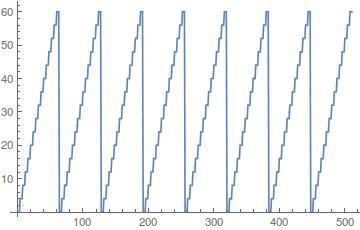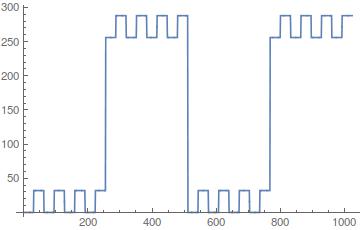
  ([0, 32, 0, 32, 0, 32, 0, 32, 256, 288, 256, 288, 256, 288, 256, 288], 512.0 length of cycles, 32.0 steps in sub-cycles)
  
  
• Some calculations: 0+32=32. 256+288=544. 256+288/32=265. 1/256+288/32=9.00390625. 32/288+256=288.125.
  
  288.125/288≃1.00043402777777777...into x*16≃16.00694444444444... ...
  
  (1/(28.8-(1/(544/6/6/6/6)*2)))/2/2/2/2/2≃0.147569444444444...==85/576. 576/85=2^6*3^2*5^-1*17^-1. ..
  
  The last entry above is called "prime factorization" which means the number can be generated by prime-number stuff. So we might try 2^6*3^2*5*7 and see what we get: 20160.
  
  Then we might try the "castled" 21600 = 20160 and divide by 512 and arrive pleasantly at 39.375..
  
  This has an inverse / reciprocal that is 0.0253968253968253968253968...
  
  Or if we are to follow page 43; 39.375*3=118.125=y. sqrt(288)*x=y.
  
  12*sqrt(2)*x-118.25=0. x≃6.696795. Though the original inverse / reciprocal divided by 6� is a repeating decimal of 4347 digits equal to 1/11022480.
  
  .. There seems to be divergence between these figures vs 39.28371 and 117.85113 on page 43 of HCOS. but..
  
  Further even if we tried ((2^6*3^2*5*7)/2/2/2/2/2/2/2/2/2)*3*x=146 then x=1168/945..
  
  Then ((2^6*3^2*5*7)/2/2/2/2/2/2/2/2/2)*3/1.125=105. Where does 105 fit in? 105*2=210..
  
  Then 216/(((2^6*3^2*5*7)/2/2/2/2/2/2/2/2/2)*3/1.125)*2=4410.
  
  
  Of course we can always make the above it slightly "pseudo" -logical so that there is no "crash" with Bruce Cathie:
  
  ((18540-((118.25-117.85113)*2*2*2*2*12*6*2*2*10))/160)=1.00044. (Skipped showing the steps of the calculation but you can find them).
  
  Thus we have 1/(1.00044/1.44)=1.439366678661388988844908240374235336451961137099676142497...
  
  
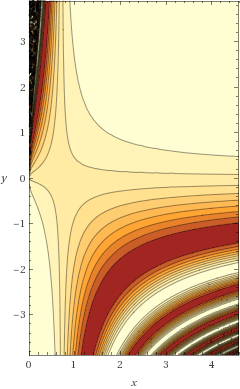
  !.. 12*sqrt(2) seems important because it shows, if we might need this fact some day, that (12*sqrt(2))**2=288. I.e the square-root of 288=12*sqrt(2)
  
  For 72 we get sqrt(6*sqrt(2)). But for 144 we have (6*sqrt(2)*sqrt(2))**2. We can go higher with (24*sqrt(2))**2=1152 which is 2^10+2^7..
  
  Not until (12*sqrt(2))**4 do we get another natural number = 82944. This maybe, suggesting 2^n for the exponential..
  
  With 1/(sqrt(12*sqrt(2))**3) we get ≃ 0.01430393849935498441548803649445.. and thus ..at least cosin(1/(sqrt(x*sqrt(2))**y)) give us art again:
  
  
  
  
• Maybe the above shows some sort of "spectral emission" i.e..
  
  

  ---

  
  
  
• But the above does not comply with the next here? Which seem like voltage drops in it..:
  
  
  
  
• First one is: [288orX], and second one is: [288xorX].
  
  
• Maybe they all should be seen as in 3D or not. Which is said to be to manipulate images with the brain..
  
  

  ---

• This is a bit special or maybe simple, as you can see for the values or harmonics of 144 like 288 shown here above. Below we try [90&x] and [60&x].
  
  
• 90 shows a sort of periodicity of 2, while 60 shows 4, possibly unclear form the images or not: